Expression =
Identifier
| AddExpression
| MultiplyExpression;
AddExpression = Expression, PlusToken, Expression;
MultiplyExpression = Expression, AsteriskToken, Expression;
このトピックでは、演算子の優先順位ルールの作成方法について説明します。
このトピックをより理解するために、以下のトピックを参照することをお勧めします。
バイナリ演算子ルールを定義する場合、グローバルなあいまいさを作成する可能性があります。詳細については、 あいまいさトピックを参照してください。
このあいまいさは、加算演算、乗算演算などの基本ルールを定義するときにも可能です。
この例は、変数の加算演算と乗算演算を処理する文章校正です。
Expression =
Identifier
| AddExpression
| MultiplyExpression;
AddExpression = Expression, PlusToken, Expression;
MultiplyExpression = Expression, AsteriskToken, Expression;
ドキュメントが「x + y * z」などのテキストを含む場合に問題があります。この場合、レクサーは次のトークンを生成します:
<Identifier, x> <PlusToken> <Identifier, y> <AsteriskToken> <Identifier, z>
以下のサブツリーの生成時にグローバルであいまいな結果になります。演算子トークンおよび「式」ノードがツリーから解除されます。
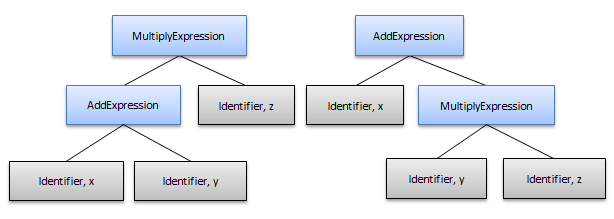
右のツリーが正しいです。乗算は加算より優先度が高く、式は x+(y*z) になります。これをサポートするには、優先度の低い演算がより優先度の高い演算の親ノードになる必要があります。
修正するには、優先レベルまたはより高い優先レベルにある演算のみである各優先レベルのオペランドを使用してルールを定義します。より優先度の高い演算は、より優先度の低い演算をオペランドとして持つことができません。また、ルールは演算子の関係を使用します。たとえば、C# の「+」は左関係です。「x + y + z」などの式は、以下の構文ツリーを生成します。
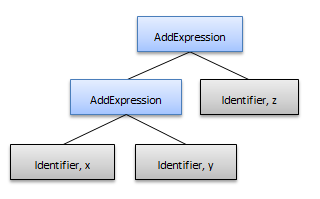
演算子の優先度および関係に基づいて、各優先レベルでルールを作成できます。以下のルールは、左関係の演算優先順位のルールです。
LowerPrecedenceExpression =
HigherPrecedenceExpression
| LowerPrecedenceExpression , OperatorToken, HigherPrecedenceExpression;
このルールは、右関係の演算のルールです。
LowerPrecedenceExpression =
HigherPrecedenceExpression
| HigherPrecedenceExpression, OperatorToken, LowerPrecedenceExpression ;
すべてのレベルが定義された後、ルートの「式」ルールは一番低い優先度を持つルールを参照する必要があります。優先度の一番低いルールは、優先度の一番低い演算またはより優先度の高い演算を表すことができます。この概念を単項、3 項、またはその他の演算に拡張できます。
以下の例は、複数の演算子を正しい優先に定義する方法を紹介します。
演算子、優先、関係
識別子、定数 - 実際のデータ
(…) - カッコ
「+、-」 - 単項プラス、マイナス (右関係)
^ - 指数 (右関係)
「*、/」- 乗算、除算 (左関係)
「+、-」 - バイナリのプラス、マイナス (左関係)
演算子の優先順位ルールの定義:
AssignmentExpression =
Identifier, Equals, Expression ;
(* メイン式記号は最低優先度を持つ記号のみを使用します * )
Expression =
AddSubtractExpression;
(* 優先レベル 6 * )
AddSubtractExpression =
MultiplyDivideExpression
| AddExpression
| SubtractExpression;
AddExpression =
AddSubtractExpression, PlusToken, MultiplyDivideExpression;
SubtractExpression =
AddSubtractExpression, MinusToken, MultiplyDivideExpression;
(* 優先レベル 5 * )
MultiplyDivideExpression =
ExponentExpression
| MultiplyExpression
| DivideExpression;
MultiplyExpression =
MultiplyDivideExpression, AsteriskToken, ExponentExpression;
DivideExpression =
MultiplyDivideExpression, SlashToken, ExponentExpression;
(* 優先レベル 4 * )
ExponentExpression =
UnaryExpression
| UnaryExpression, CaretToken, ExponentExpression;
(* 優先レベル 3 * )
UnaryExpression =
ParenthesizedExpression
| UnaryPlusExpression
| UnaryMinusExpression;
UnaryPlusExpression =
PlusToken, UnaryExpression;
UnaryMinusExpression =
MinusToken, UnaryExpression;
(* 優先レベル 2 * )
ParenthesizedExpression =
PrimaryExpression
| OpenParen, Expression, CloseParen;
(* 優先レベル 1 * )
PrimaryExpression =
Identifier
| Constant;
この方法のマイナス面は、「x = y」などの簡単な式の場合に大きい構文ツリーを作成します。
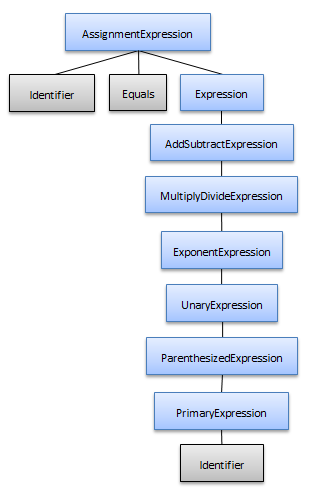
このトピックの追加情報については、以下のトピックも合わせてご参照ください。